El estudio de cómo se expanden las ciudades ha sido un área de investigación muy activa durante las últimas décadas. Una de las consecuencias principales de esta expansión ha sido el deterioro del entorno y los problemas sociales.
Con el objetivo de solucionar estos problemas, la Comisión Europea presentó en los años 90 el concepto de ciudad compacta, en base al cual las ciudades se caracterizan por áreas de muy alta densidad con un uso del terreno multifuncional y una forma urbana compacta. Sin embargo, este concepto también tiene sus limitaciones, siendo la principal la presión que sufren el centro de las ciudades y sus consecuencias en los precios residenciales y en el deterioro social.
El concepto de ciudad compacta no se refiere únicamente a densidad urbana sino también a la estructura de la misma, entendida como la interrelación entre los diferentes centros de actividad. Los centros de actividad (o hotspots) se refieren a las áreas más prolíficas en actividad económica y social, y pueden ser considerados como el componente estructural principal de las ciudades.
Cómo de bien funciona una ciudad dependerá de la cantidad, la distribución y el número de enlaces entre los centros de actividad de manera que cada parte individual tenga su función en la red urbana y se integre en el concepto global de la ciudad. Surge entonces la pregunta sobre cuál debe ser la cantidad y la distribución de estos centros de actividad para maximizar el rendimiento de un entorno urbano.
El estudio de entornos urbanos se realiza típicamente mediante datos socioeconómicos de alta resolución o mediante trazas de teléfonos móviles. No obstante, otras fuentes de información tales como las imágenes vía satélite, especialmente las de luminosidad nocturna, son muy interesantes debido a su disponibilidad fácil y global.
Considerando imágenes de luminosidad nocturna recogidas por el Defence Meteorological Satellite Program’s Operational Linescan System (DMSP-OLS) de 349 ciudades estadounidenses, 239 europeas y 276 chinas, hemos realizado una serie de experimentos para ver cuál debe ser la distribución óptima de centros de actividad en una ciudad para maximizar su producción económica.

Para cada una de las ciudades consideradas se identificaron los centros de actividad utilizando el método de Loubar. A partir de los centros de actividad identificados para cada ciudad, primero se estudió la relación entre el número de centros de actividad con la población.
La Figura 1 presenta para cada una de las áreas geográficas consideradas (azul para ciudades norteamericanas, verde para ciudades europeas y rojo para ciudades chinas), cada ciudad con su número de centros de actividad y su población.
El factor de escala (pendiente de la recta en escala log-log) es en los tres casos muy parecido: entre 0.51 y 0.55. Este factor de escala común indica que todas las ciudades tienden a comportarse de la misma manera al crecer, mostrando que, si se duplicase la población, el número de centros de actividad se incrementaría un 50%, o lo que es lo mismo, que cuanto más grande es la ciudad, más población puede soportar sus centros urbanos.
Este resultado referente a cómo crecen las ciudades está en línea con el estado del arte, por ejemplo, en un trabajo anterior se encontró un factor de escala de 0.54 para las ciudades españolas más pobladas utilizando trazas de teléfonos móviles. En general, estos resultados indican que el crecimiento de las ciudades sigue una ley universal de escala sub-lineal.
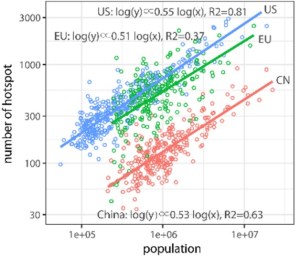
Aunque los exponentes son muy similares, las ciudades de las distintas áreas geográficas se comportan de forma muy diferente. Respecto al coeficiente R2, que indica cómo de bien aproxima el modelo lineal los datos disponibles, las ciudades norteamericanas son muy homogéneas, con un valor de 0.81, mientras que la mayor dispersión se encuentra en las ciudades europeas, con un valor de 0.37. La diferencia más relevante es en lo relativo a los valores de corte: por ejemplo, para una población de 1 millón de habitantes, el número de centros de actividad es muy diferente, en torno a 130 para las ciudades chinas, 650 para Europa y 720 para las ciudades de Estados Unidos.
Es decir, en China, las áreas de actividad soportan una densidad de población considerablemente superior a los casos de Estados Unidos y Europa. Si se considerase un único modelo para las tres áreas geográficas, el modelo lineal tendría un R2 de 0.09, es decir, que el modelo explicaría sólo el 9% de la variabilidad de los datos. Esto indica que la población, por si sola, no explica la variación en el número de centros de actividad.
La hipótesis de nuestro estudio es que uno de los factores más relevantes que define el número y la interacción entre los centros de actividad es el nivel de desarrollo económico. Estudios anteriores ya indican que las ciudades con un nivel de vida más alto tienen menor densidad de población.
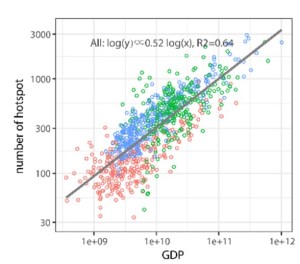
La Figura 2 presenta la correlación entre el GDP (Producto Interno Bruto, PIB) de todas las ciudades de las tres áreas geográficas consideradas y el número de centros de actividad. En este caso, considerando globalmente todas las ciudades, la regresión produce un R2 de 0.64, es decir, que el GDP puede explicar mas de la mitad de la variación en el número de centros de actividad. Estos resultados ponen de manifiesto que es el GDP, y no el tamaño, el que tiene una mayor importancia respecto a la generación de centros de actividad.
Cabe entonces preguntarse cuál es la relación entre la forma de una ciudad y su GDP. Para caracterizar la forma de una ciudad, necesitamos usar métricas que midan como están distribuidos los centros de actividad. Entre varias métricas posibles, para este estudio usamos el índice de proximidad entre centros de actividad, definido como la ratio entre el diámetro de un círculo con la misma área que el conjunto de centros de actividad detectados y la máxima distancia entre esos centros de actividad. El valor varía entre 0 y 1 (valores próximos a 1 indica que los centros de actividad están muy cercanos entre sí, y próximos a 0 que se dispersan en la ciudad).
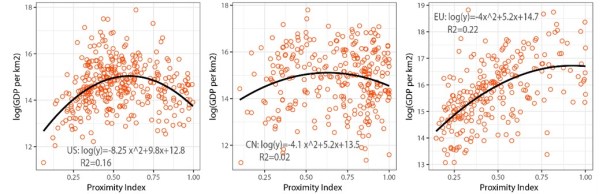
Obteniendo el índice de proximidad para cada ciudad, la Figura 3 presenta el índice respecto al GDP para los casos de Estados Unidos, China y Europa, respectivamente. Usando un modelo de regresión cuadrática, se puede observar un comportamiento de U invertida que implica que, respecto al GDP, se alcanza un valor máximo, y que por tanto es posible diseñar una ciudad con un índice de proximidad en mente entre sus centros de actividad para poder maximizar el GDP. En el caso de Estados Unidos y China, el índice de proximidad ideal está entre 0.5 y 0.75 (con máximos en 0.61 y 0.63 respectivamente) aunque las ciudades chinas muestran una mayor dispersión respecto al GDP y tienden a tener índices de proximidad más altos.
En el caso de las ciudades europeas no hay tanta diferencia entre el modelo lineal y el modelo cuadrático, lo que implica que no se alcanza ese máximo de forma tan clara. Esto es debido a una variedad de factores, siendo el principal que las ciudades norteamericanas y las chinas son más recientes, y por tanto siguieron desde su creación alguna política de diseño. Este no es el caso de la mayoría de las ciudades europeas.
En general, los resultados indican que centros de actividad muy cercanos entre si tienden a crear congestión y que los muy lejanos tienen problemas de conectividad, resultando en ambos casos en una disminución del GDP. El valor del índice de proximidad ideal que se debe considerar al diseñar una ciudad para maximizar el GDP debería situarse en torno a 0.6.
Los resultados obtenidos indican la posibilidad de diseñar una ciudad de forma óptima conforme a un objetivo, maximizar el GDP en este caso. Asimismo, el estudio demuestra que el uso de imágenes de luminosidad nocturna es de utilidad para estudiar y caracterizar ciudades.
El reto se presenta ahora en cómo combinar estas imágenes con otras informaciones (tales como datos de móviles, valores demográficos y socio-económicos, o información pasiva de red) de forma relevante, para poder construir herramientas para el estudio y diseño de ciudades.









