En su libro [The Perfect Thing](https://www.amazon.es/Perfect-Thing-Shuffles-Commerce-Coolness-ebook/dp/B000MGATVC/ref=as_li_ss_tl?s=books&ie=UTF8&qid=1563253968&sr=1-6&linkCode=sl1&tag=elartdepre-21&linkId=ee5d3be1a94982b2d3d40a320681a482&language=es_ES), Steven Levy (el famoso autor de [Hackers: Heroes of the Computer Revolution](https://amzn.to/2k0jRTZ) y [Crypto: Secrecy And Privacy In The New Cold War](https://amzn.to/2jWIZLj) nos describe cómo empezó a darse cuenta de que había canciones, e incluso artistas, que **a su iPod no le gustaban**.
Investigando el asunto comprobó que no era el único que creía que su iPod tenía preferencias propias. Daba la impresión de que casi todos los iPods parecían tener un artista favorito, o dos, o tres, ya que cuando reproducía de forma aleatoria (en modo shuffle), su iPod decidía qué artista le apetecía y luego se dedicaba a poner los trabajos de ese intérprete.
Rápidamente, la gente saltó a dar explicaciones parapsicológicas (“pienso en una canción o en un grupo y mi iPod lo reproduce”) y hasta conspiranoicas (“Apple prohíbe al iPod reproducir canciones de este grupo porque es de derechas”). En cambio, Levy intentó analizar racionalmente lo que podría estar pasando: ¿por qué los ingenieros de iPod afirman que el modo shuffle es “absolutamente, inequívocamente aleatorio”, pero se comporta como si tuviera voluntad propia y estados de ánimo? ¿Hay un fantasma en la máquina?
Levy consultó a John Allen Paulos, un matemático de la Universidad Temple de Filadelfia, quien le explicó cómo “a menudo interpretamos e imponemos patrones a eventos que son aleatorios. Especialmente con algo como canciones. Las canciones evocan emociones y algunas se quedan en nuestras mentes más que otras. (…) Nuestros cerebros no están diseñados para comprender la aleatoriedad“.
Levy concluyó que cuando pensamos que el modo shuffle del iPod no es aleatorio, el problema está en nuestras percepciones. Nuestras mentes perciben patrones y tendencias que realmente no existen. A menudo escuchamos series de canciones consecutivas del mismo artista y pensamos que no es aleatorio, aunque, de hecho, con verdadera aleatoriedad, tales secuencias consecutivas son mucho más probables de lo que cabría esperar.
La percepción incorrecta de la aleatoriedad empujó a Apple a introducir la función Smart Shuffle en una nueva versión de iTunes. Con esta característica, se evitan las secuencias consecutivas del mismo artista. Según declaró Steve Jobs en su día:
“Lo hacemos menos aleatorio para que se perciba como más aleatorio”
La noche en el casino de Montecarlo en la que cientos perdieron millones
La noche del 18 de agosto de 1913, algo inusual ocurrió en una mesa de ruleta del casino de Montecarlo. Algunos jugadores notaron que la bolita había aterrizado en negro durante 10 giros seguidos de la rueda. La gente comenzó a congregarse alrededor de la mesa. Diez negros seguidos es una secuencia excesivamente larga. Necesariamente, debería caer en rojo en la próxima ronda. Así que los jugadores comenzaron a apostar agresivamente al rojo. La rueda giró de nuevo… ¡Y la bolita cayó en negro por undécima vez consecutiva!
Al igual que en la duodécima… Y decimotercera… Y decimocuarta… Y cuanto más duraba la racha de negros, más convencidos estaban los jugadores de que la próxima vuelta produciría necesariamente un rojo. El valor de sus apuestas al rojo se incrementó. Sus pérdidas se dispararon.
¡La bolita aterrizó 26 veces consecutivas en negro! La probabilidad de ocurrencia de tal secuencia es (18/37)26 o alrededor de 1 en 66,6 millones, suponiendo que el mecanismo no esté trucado.
Para cuando cayó finalmente en rojo en la ocasión vigesimoséptima, la mayoría de los jugadores estaban completamente arruinados. Pero, ¿qué crees que hicieron los que aún conservaban capital?
Pues apostar una y otra vez al rojo, persuadidos de que a una racha tan larga de negros necesariamente habría de seguirle una racha igualmente larga de rojos para compensar. Por supuesto, no fue así. Los pocos que no lo habían perdido todo en la racha de negros, lo perdieron en la inexistencia de racha de rojos. Aquella noche tal vez fue la más rentable en la historia del casino: se perdieron fortunas y nació la “falacia de Montecarlo”.
La “falacia de Montecarlo”, también conocida como “falacia del jugador”, recoge la idea de que el comportamiento pasado influye en el comportamiento futuro. Puede comprender las siguientes ideas equivocadas:
Un suceso aleatorio tiene más probabilidad de ocurrir porque no ha ocurrido durante cierto período.
Un suceso aleatorio tiene menos probabilidad de ocurrir porque ha ocurrido durante cierto período.
Un suceso aleatorio tiene más probabilidad de ocurrir si no ocurrió recientemente.
Un suceso aleatorio tiene menos probabilidad de ocurrir si ocurrió recientemente.
Este error de juicio se produce porque por algún extraño mecanismo inconsciente atribuimos memoria a los objetos. Si lanzas una moneda al aire y salen 10 caras seguidas, la probabilidad de que salga cara la próxima vez sigue siendo 1/2, por mucho que haya salido cara las 10, 100 o 1.000 veces anteriores. Pero nos resistimos a creer que siga siendo 1/2 porque pensamos:
“¿Cuál es la probabilidad de que salga cara 10 veces seguidas? Es bajísima (concretamente, de 1/1024). Por lo tanto, la próxima tiene que salir cruz”.
Por desgracia, el azar no es un proceso justo que se corrige a sí mismo para compensar rachas largas. Ni la ruleta ni la moneda guardan memoria. Cuando observamos una serie corta de eventos aleatorios independientes, cualquier secuencia puede producirse, por desviada de la media que esté. Se puede culpar a la heurística de representatividad como responsable de esta distorsión cognitiva: la gente cree que las secuencias cortas de eventos aleatorios deberían ser representativas de eventos más largos. Como explicamos al hablar sobre la regresión a la media, la realidad no funciona así.
Los dioses hablan, los espíritus hablan, los ordenadores hablan
Sucumbimos a esta falacia allí donde el azar esté involucrado. Leí en la revista Nautilus la curiosa historia de Sid Meier, el diseñador del popular juego Civilization.
Cuenta cómo las pruebas de validación del juego revelaron el siguiente hecho paradójico: si a un jugador se le dice que tiene una probabilidad de éxito del 33% en una batalla, pero luego no puede derrotar a su oponente tres veces seguidas, se vuelve furioso e incrédulo. Así que Meier alteró el juego para sintonizarlo con los sesgos cognitivos humanos: si tu probabilidad de ganar una batalla es de 1/3, el juego te garantiza que ganarás como tarde en el tercer intento. ¡Ah, qué paradoja! Una tergiversación de la probabilidad real que, sin embargo, ofrece la ilusión de justicia divina.
La profesora de matemáticas Deborah Bennet, autora de Randomness cierra su obra con estas palabras que resumen a la perfección nuestra incapacidad de manejar la aleatoriedad:
“A corto plazo, el azar puede parecer volátil e injusto. Y aunque la experiencia con largas series puede ayudar a modificar algunos de nuestros sesgos cognitivos basados en un malentendido de la aleatoriedad y la probabilidad, puede requerirse una secuencia muy larga. Teniendo en cuenta los conceptos erróneos, las inconsistencias, las paradojas y los aspectos contraintuitivos de la probabilidad, no debería sorprendernos que, como civilización, tardamos largos años en desarrollar intuiciones correctas. De hecho, todos los días podemos ver evidencia de que la especie humana aún no tiene un sentido probabilístico muy desarrollado. Quizás todos deberíamos abordar los encuentros casuales con precaución, a corto plazo.”
La aleatoriedad tal y como la imaginamos se manifiesta en los grandes números, no en los pequeños números.
Para el ojo no entrenado la aleatoriedad aparece como regularidad o tendencia a la agrupación
Si disparas dardos con los ojos cerrados a una diana cuadrada dividida en una cuadrícula de 10×10, ¿cómo se distribuirán esos impactos aleatorios?
He realizado el experimento programando 10 disparos al azar. El resultado se muestra en la siguiente figura:
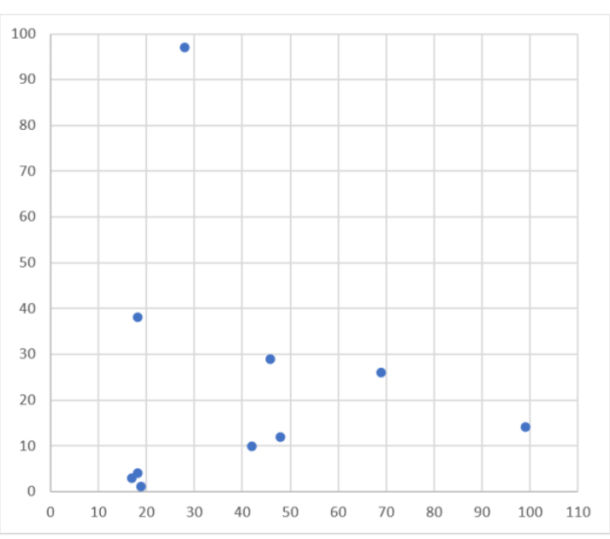
Un tanto sospechoso, ¿no? Todos los dardos menos uno se encuentran por debajo de la línea 40. Además, una casilla ha recibido tres disparos y otra, dos. ¿Seguro que será aleatorio? En nuestra imaginación, confundimos “aleatorio” con “uniformemente distribuido”.
Pasemos de los dardos a las monedas. Si se lanza al aire una moneda sin trucar seis veces seguidas, representando «cara» con un 1 y «cruz» con un 0, aparecerán secuencias de lo más variado, como por ejemplo las siguientes:
1. 1 0 1 0 1 0
2. 1 1 1 1 1 1
3. 1 0 1 1 0 1
Reconócelo. ¿No te parece más aleatoria la tercera secuencia, 1 0 1 1 0 1? Las dos primeras parecen demasiado ordenadas, ¿verdad? No coinciden con nuestra idea intuitiva de aleatoriedad. En realidad, las tres secuencias son equiprobables, con una probabilidad de (1/2)6 = 1/64. Pero como estamos más acostumbrados a ver secuencias desordenadas que ordenadas (porque de hecho hay más), de alguna manera la tercera secuencia es la que mejor representa nuestra imagen preconcebida de cómo debe ser la aleatoriedad. Sin embargo, para que una secuencia aleatoria nos parezca aleatoria no podemos observar unas pocas instancias, sino muchas.
Así que volvamos a la diana. ¿Qué pasa si lanzamos 100 dardos? Poniendo a trabajar al ordenador ofrece este nuevo resultado. ¿Parece más aleatorio ahora?
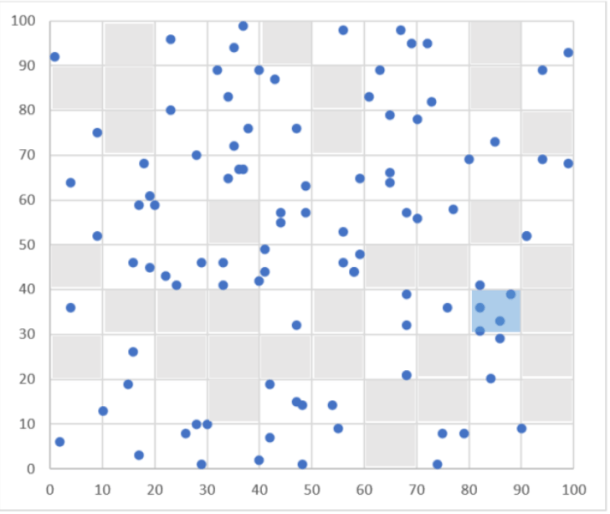
Aquí ya hay quien empieza a ponerse nervioso. ¡Hay 33 recuadros no visitados! En otras palabras: no ha caído ni un solo dardo en un tercio de la diana. Es más, en un recuadro han aterrizado nada menos que 4 dardos.
“Hmmm, aquí pasa algo raro. Si los disparos son aleatorios, ¿no deberían haberse distribuido por todo el tablero?”
De nuevo, confundimos aleatoriedad con uniformidad. Sí, efectivamente, se distribuirán por todo el tablero… ¡Cuando el número de disparos sea suficientemente alto!
¿Serán 1.000 dardos un número suficientemente alto? Veámoslo.
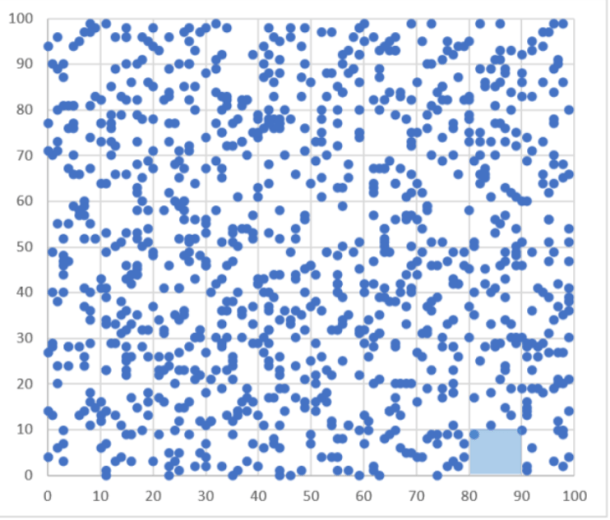
Nos vamos acercando. Por puro azar, un recuadro (señalado en la imagen) solo ha recibido un dardo, mientras que otros han recibido incluso más de 10. Por supuesto, cada vez que se repita el experimento se obtendrá una distribución diferente, pero estadísticamente similar. Es más, repítelo un número suficientemente alto de veces y hasta terminará apareciendo la cara de Mona Lisa o del mismísimo pato Donald.
La pareidolia no es más que eso: ver figuras antropomorfas en las nubes, vírgenes en las manchas de humedad de la pared o rostros humanos en las formaciones geológicas de Marte. Nuestro cerebro detecta orden donde no existe. Si la Naturaleza aborrece el vacío, los seres humanos aborrecemos el desorden.
Durante miles de años hemos conectado con la imaginación las estrellas del cielo para recrear todo tipo de constelaciones. La mente humana es una fabulosa herramienta de búsqueda de sentido. Somos extraordinarios reconociendo patrones, viendo caras en cualquier disposición aleatoria de objetos o dando sentido a distribuciones aleatorias que no lo tienen.
Volvamos a la diana anterior. Imagínate que en realidad es el plano de una ciudad y los diez puntos de la Figura 1 representan casos de un raro cáncer registrado en los últimos cinco años. Claramente, están concentrados en un barrio, ya que afecta a un área muy restringida del mapa. Si quiere la casualidad que en ese barrio se haya levantado una antena de telefonía móvil o cualquier construcción “sospechosa”, ¡la polémica está servida! Sin embargo, toda inferencia carece de relevancia estadística.
Esta tendencia a considerar erróneamente como no aleatorias las inevitables “rayas” o “grupos” que surgen en pequeñas muestras de distribuciones aleatorias se conoce como la “ilusión de agrupamiento”. La ilusión es causada por nuestra tendencia a subestimar la cantidad de variabilidad que probablemente aparezca en una pequeña muestra de datos aleatorios o semialeatorios.
Ignorar el papel del azar puede conducir a decisiones desastrosas
“Durante el intenso bombardeo de Londres en la Segunda Guerra Mundial, generalmente se creyó que los bombardeos podrían no ser aleatorios porque un mapa de los impactos revelaba la existencia de llamativas zonas indemnes.
Algunos sospecharon que en estas zonas no afectadas había espías alemanes. Un cuidadoso análisis estadístico reveló que la distribución de los impactos era la habitual de un proceso aleatorio, y la habitual también en provocar una fuerte impresión de que no se producía al azar”
Esta historia narrada por el famoso psicólogo Daniel Kahneman en su libro Pensar rápido, pensar despacio viene a ilustrar nuestra necesidad de imponer orden a nuestro alrededor y de buscar explicaciones causales para todo, incluso para fenómenos de naturaleza aleatoria. En el fondo, es como aquel pistolero que disparaba a la pared del granero y después dibujaba la diana alrededor de los disparos.
Examina de nuevo la Figura 2. Si correspondiera al mapa de los bombardeos, ¿qué pensarías de las zonas marcadas en azul? ¿Serían nidos de espías? No. Como ya hicieron nuestros antepasados observando el cielo nocturno, nuestra necesidad de dotar de sentido a la realidad nos ciega al razonamiento estadístico y nos impulsa también a conectar los puntos aleatorios con una buena historia. Por desgracia, las explicaciones causales de acontecimientos aleatorios son inevitablemente falsas.
Buscamos patrones. Creemos en un mundo coherente en el que las regularidades aparecen no por accidente, sino como resultado de la causalidad mecánica o de la intención de alguien. No esperamos ver la regularidad producida por un proceso aleatorio. Y cuando detectamos lo que parece ser una regla, rápidamente rechazamos la idea de que el proceso es verdaderamente aleatorio. Los procesos aleatorios producen muchas secuencias que convencen a las personas de que el proceso no es aleatorio, después de todo.
Y si no, que se lo pregunten al Sr. Jobs y a su modo Smart Shuffle.









